Un vaste sujet avec quelques pistes
Catégorie : 1 S2 curiosités pb de recherche
Des exercices plus “fouillés”, des éléments de culture scientifique , pour les curieux
des problèmes d’ordre
Une vidéo intéressante à écouter et à réfléchir est éclairante sur les phénomènes d’ordre même pour la vie courante l’auteur peut être suivi sur youtube.
pb d’entrainement révisions
Un premier pb sur le second degré corrigé
Télécharger (2015-2016 DS1g.pdf)
Un second sur les vecteurs
Télécharger (AA1sDsT03_Vecteurs.pdf)
et son corrigé
Une pluie de météorite le 14 et 15 décembre
Géminides 2015 : belle pluie d’étoiles filantes à observer
 |
| Ciel le 14 décembre 2015 à 23h |
C’est en direction de l’Est-Sud-Est qu’il faudra plutôt regarder. Evitez de regarder en direction du Nord où vous en apercevrez moins. Mais il ne faut pas se focaliser non plus sur le radiant. Observez toutes les constellations faciles à reconnaître qui se trouvent autour de celle des Gémeaux : Le Cocher, son hexagone caractéristique et son étoile très brillante (Capella) vers le zénith, Orion et ses trois étoiles alignées formant son baudrier vers le Sud, ou le Lion vers l’Est.
Vous devrez d’ailleurs laisser un peu de temps à vos yeux pour s’habituer à l’obscurité, environ 15 à 30 minutes, puis en réduisant au maximum le recours à une lampe (si nécessaire préférez une lampe rouge ou orange plutôt qu’un écran de téléphone blanc/bleuté, qui nécessitera une nouvelle acclimatation à l’obscurité plus longue).
N’hésitez pas à observer entre amis en jouant pourquoi pas à celui qui verra un maximum d’étoiles filantes ou de satellites…. Entre deux météores, vous pourrez observer tranquillement les constellations du ciel d’hiver, et par exemple Orion, où vous pourrez essayer de distinguer à l’oeil nu la grande nébuleuse, située légèrement en dessous des trois étoiles du baudrier. Vous verrez probablement passer des satellites, qu’il ne faut pas confondre avec des météores, les satellites ont un éclat constant et se déplacent à vitesse constante relativement lente durant plusieurs secondes, les météores, eux, sont très rapides et parfois très fugaces…
Si vous souhaitez prendre des photos, préférez l’objectif le plus petit (24 ou 35 mm), avec la plus grande ouverture possible (du genre f/2.8), avec un réglage sur ISO 800 ou plus. Utilisez un trépied et répétez de multiples poses de 30 s ou 1 minute, en espérant que la chance sera de votre côté et que vous capturerez un ou plusieurs bolides multicolores…
 |
| L’astéroïde 3200 Phaeton imagé par STEREO en 2012 à son point le plus proche du Soleil, montrant une queue de poussières (NASA/STEREO) |
Une recherche sportive
Des maths pour courir plus vite
Achille ne rattrapera jamais la tortue, les paradoxes du philosophe grec Zénon d’Élée nous le disent depuis 2500 ans. Mais Achille peut progresser: les équations de deux mathématiciens français lui permettraient d’optimiser sa vitesse et l’énergie dépensée en courant.
Amandine Aftalion ne court pas, elle nage. Et lorsqu’elle nage, la directrice de recherche CNRS au laboratoire de mathématiques de Versailles (université de Versailles-Saint-Quentin) réfléchit. Il y a trois ans, en plein dos crawlé, elle a songé à ses lectures sur la physiologie du sport et a pensé que «les mathématiques devaient pouvoir expliquer la physiologie de l’exercice».
La physique en équations
Joseph Keller, de l’université de New York, avait tâté le terrain dans les années 1970 et défini une course de fond idéale, en trois temps: brusque accélération, vitesse constante pendant la majeure partie de la course, puis décélération finale. Mais Keller et ses successeurs se basaient sur des valeurs moyennes, omettant que vitesse et capacité respiratoire varient lors d’une course.
Avec Frédéric Bonnans, directeur de recherches Inria au centre de mathématiques appliquées (École polytechnique), Amandine Aftalion a donc mis en équations les bases de la physique. Principe numéro un: rien ne se perd, rien ne se crée ; faire la somme des énergies disponibles (oxygène et glucose, pour faire simple) permet donc de savoir ce que l’on peut dépenser. Principe numéro deux, la variation de la vitesse est égale à la somme des forces en présence. «On nomme toutes les variables, on écrit les équations et on calcule», résume la chercheuse.
Varier sa vitesse pour courir longtemps
Son modèle mathématique confirme une réalité bien connue des coureurs: varier (un peu) sa vitesse permet de courir plus longtemps, chaque décélération permettant de restocker un peu d’énergie pour accélérer de plus belle. Ces variations sont inconscientes, mais une prise de mesures tous les 50 ou 100 mètres montre que la vitesse de course oscille, par exemple entre 5,5 et 6,5 mètres par seconde lors d’un 1 500 mètres. Oscillations qui permettent au coureur de garder un peu d’énergie pour mieux finir sa course… ou pour aller plus loin. Selon l’étude bientôt publiée dans le Journal of Applied Mathematics (et déjà disponible sur les archives ouvertes HAL), le gain offert par une variation optimale de la vitesse serait de 0,7 % du temps de course sur 800 mètres. Ces équations font aussi de l’ordinateur un véritable coach sportif, plus performant que les outils d’automesure qui inondent le marché.
Prenez donc la capacité respiratoire (VO2max) et le stock d’énergie anaérobie (due à la transformation des sucres) d’un coureur ; ajoutez-y sa vitesse maximum, ses capacités d’accélération, sa force de propulsion et les forces de frottement auxquelles ses muscles sont soumis. Quelques courses types permettront au logiciel de calculer ces paramètres, propres à chacun. Muni de ces variables (et partant du principe que le coureur… avance!), le système nous indique quelles capacités développer pour cavaler comme un champion, et comment courir au mieux sur une distance donnée. L’ordinateur donnera donc à l’amateur ce qu’un bon coach et l’expérience apportent aux champions. Plus prosaïquement, le sportif saura aussi combien de calories il a exactement dépensées lors de son effort.
Amandine Aftalion admet tout de même que «pour résoudre plusieurs équations en même temps, il faut disposer de techniques de résolution numérique très avancées». Proposer son système aux coureurs du dimanche supposera donc de trouver des partenaires industriels, pour développer un programme capable de tourner sur l’ordinateur d’Achille. Qu’il puisse enfin doubler cette satanée tortue.
Travaux d’Amandine Aftalion, partiellement en collaboration avec F. Bonnans sur la modélisation mathématique de la physiologie de la performance pour ceux qui veulent en savoir plus un exemple de travaux en Français
Amandine AftalionCNRS Research Director Professor at Ecole Polytechnique Office 3308 (Building Fermat) |
A partir d’équations mathématiques, nous avons développé avec F.Bonnans, chercheur à l’inria, un modèle qui est capable de prédire comment doit se dérouler la course optimale, une fois qu’on a décidé de la distance à parcourir. Nous savons calculer à chaque instant, la vitesse que doit avoir le coureur et l’énergie qu’il a dépensé depuis le début de la course. Pour des courses allant du 400m au marathon, nos résultats amènent en particulier à 2 conclusions qui renforcent certaines observations physiologiques :
* le negative split: il vaut mieux courir la 2ème partie de la course plus vite que la première
*il faut varier sa vitesse, ce qui permet de gagner par exemple 0.7% sur 800m. En effet, quand on ralentit, on recrée un peu d’énergie, ce qui permet d’améliorer son temps de course.
Sur les marathons par exemple, les coureurs sont invités à choisir une couleur en fonction de leur temps de course espéré (2h30, 3h, 4h, 5h etc). Cette couleur est associée à un ballon ou lièvre qui va se déplacer à vitesse constante pour arriver à la fin de la course dans le temps escompté. Et pourtant, tout coureur qui a couru un marathon s’est rendu compte qu’il avait envie de varier sa vitesse, en accélérant puis ralentissant. Oui, c’est normal, c’est ainsi que l’organisme arrive à régénérer un peu d’énergie.
Comment arriver à calculer à chaque instant la vitesse et l’énergie disponibles pour un coureur? Cela nécessite un système d’équations différentielles, c’est-à-dire des équations reliant la vitesse (et sa dérivée l’accélération), la force de propulsion, les forces de frottement et l’énergie. Les équations reposent sur le principe fondamental de la dynamique et des bilans d’énergie faisant intervenir notamment VO2max, la consommation maximale d’oxygène du coureur, et les liens de contrôle entre ces variables : par exemple, la recréation d’énergie quand on ralentit. Pour être bien posé, le système est couplé à des conditions initiales (vitesse nulle et énergie donnée au départ) et des contraintes : l’énergie doit rester positive, la force de propulsion aussi (on ne recule pas !) et cette force est bornée par les capacités limitées du coureur ; enfin la dérivée de cette force de propulsion est bornée aussi car les informations ont besoin de temps pour passer du cerveau à la jambe : le coureur ne peut pas instantanément comme un ordinateur, passer d’une force de propulsion maximum à l’arrêt complet. Le travail de modélisation consiste à bien poser ce système. Mathématiquement, nous arrivons à prouver des théorèmes sur le comportement des solutions. En particulier, quand on rajoute un terme de recréation d’énergie due au ralentissement, on se rend compte que cela crée des termes concaves dans le hamiltonien qui sont à l’origine des oscillations de vitesse. Enfin, numériquement, nous sommes capables de résoudre ce système d’équations pour calculer les valeurs de toutes les variables intéressantes pour le coureur et les relier aux mesures physiologiques. Nos simulations numériques nécessitent une programmation complexe et jamais réalisées sur ce type d’exemples. Elles utilisent le logiciel Bocop ( voir http://bocop.org/ pour les très curieux) , qui nous a permis de résoudre le système d’équations différentielles couplées, sous contraintes, et avec contrôle optimal.
A quoi cela pourrait-il servir ? On se pose souvent la question de : à quoi servent les mathématiques? Les applications en sont pourtant immenses. Dans le cas de la course à pied, on pourrait, à partir des équations que nous avons établies, imaginer un logiciel qui calcule sur un smart-phone
*la vitesse optimale de course et donne des indications au coureur sur des bases scientifiques
* la dépense énergétique et permet de voir comment elle aurait pu être meilleure. On peut alors savoir exactement le nombre de calories perdues lors d’une course, et pas avec une estimation moyenne comme le font tous les calculs actuels, mais véritablement avec un calcul exact instantané.
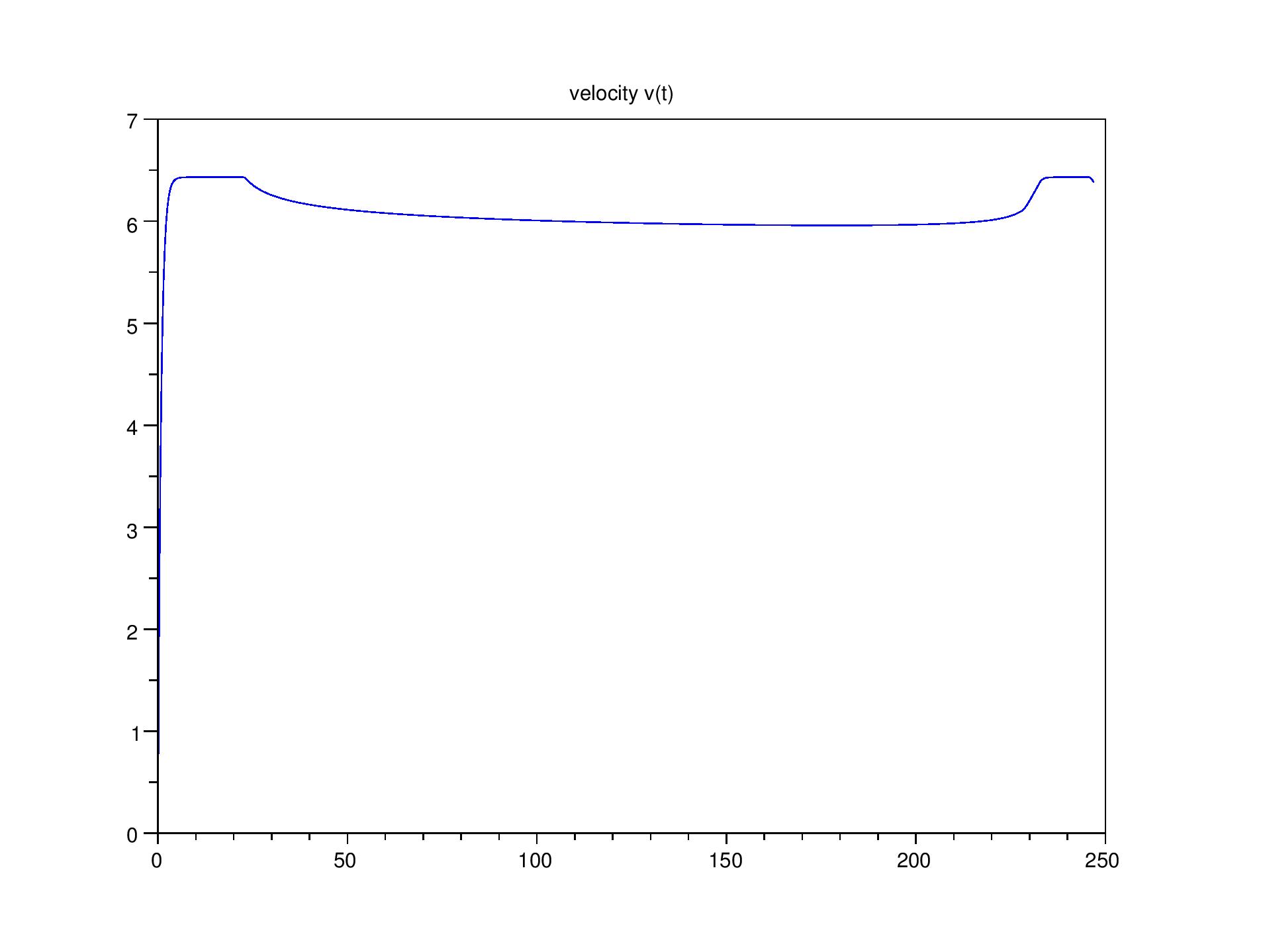 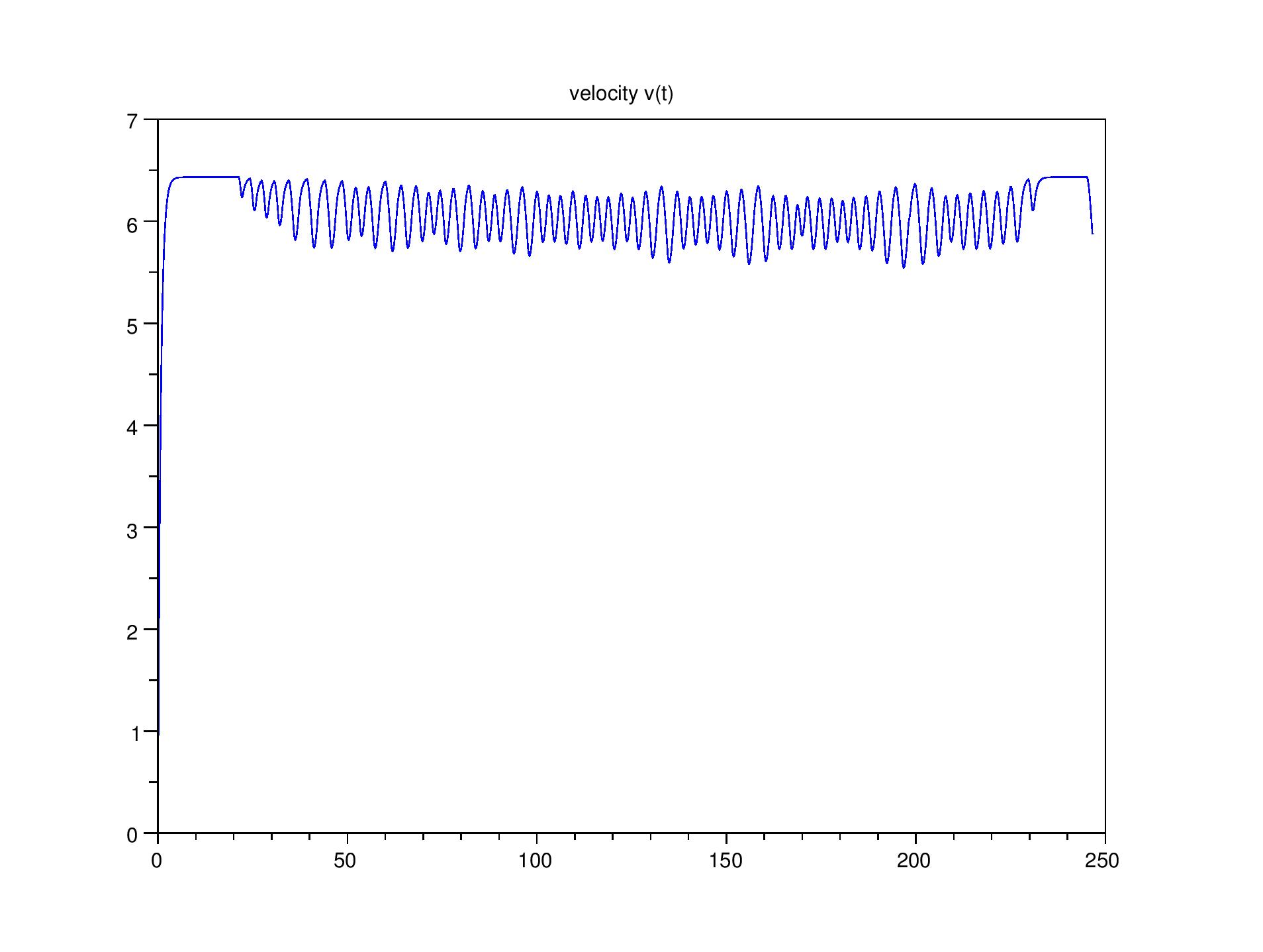 |
A gauche : sur un 1500m, profil de vitesse sans prendre en compte la recréation d’énergie quand on ralentit (on tient juste compte de la chute du VO2max en fin de course quand la réserve d’énergie anaérobie est trop faible)
A droite : quand on prend en compte la recréation d’énergie en ralentissant, la vitesse oscille.
« En cheminant avec Kakeya », Prix Tangente 2015
« En cheminant avec Kakeya », Prix Tangente 2015
Le « Prix Tangente 2015 » vient d’être décerné à Vincent Borrelli et à Jean-Luc Rullière, pour leur livre « En cheminant avec Kakeya » (ENS éditions) livre qui contient ce qu’il faut pour structurer la pensée de lycéens de terminale ou d’étudiants, pour instiller un peu de piment dans leurs mathématiques, les sortir de la routine… Les inciter à la réflexion, quoi ! ![]()
Pour nous en première avant cette lecture recommandée pour la terminale je vous propose (pour les plus curieux d’entre vous une approche de ce théorème ainsi qu’une vidéo qui vous permettra d’entrevoir une démarche scientifique sous un autre angle (‘et vous fera réviser votre anglais ![]() et oui … en fait même sans vraiment tout comprendre de l’anglais on comprend l’esprit de la démonstration qui elle est limpide et géniale
et oui … en fait même sans vraiment tout comprendre de l’anglais on comprend l’esprit de la démonstration qui elle est limpide et géniale ![]() . durée 16 min pour les pressés vous pouvez démarrer à la 6 ième car la mise en place ne fait que rappeler quelques propriétés des aires.)
. durée 16 min pour les pressés vous pouvez démarrer à la 6 ième car la mise en place ne fait que rappeler quelques propriétés des aires.)
En 1917, le mathématicien japonais Sôichi Kakeya posait une question apparemment anodine :
existe-t-il une plus petite surface (en terme d’aire ) à l’intérieur de laquelle il serait possible de déplacer une aiguille de manière à la retourner complètement ?
La première surface qui vient vraisemblablement à l’esprit est un disque, dont l’aiguille serait un diamètre : en pivotant de 180° autour du centre de ce disque, elle balaie le disque sans jamais en sortir… Et se retourne.
Mais est-ce la plus petite surface ?
Ce n’est qu’en 1928 – 11 ans plus tard – que le mathématicien (russe, celui-là : les mathématiques n’ont pas de frontières) Abram Besicovitch prouva que :
Non : il est possible de retourner une aiguille dans une surface dont l’aire est aussi petite que l’on veut.
Prouva ! Ce n’est pas de la prestidigitation… C’est de la science !!!:lol:
C’est tout le cheminement vers ce théorème de Besicovitch que raconte ce « voyage au cœur des mathématiques » de Vincent Borrelli et Jean-Luc Rullière…
Prenez le temps de regarder cette vidéo de « Mathologer », qui propose une animation graphique que je trouve merveilleusement claire du « problème de l’aiguille de Kakeya »… En remplaçant l’aiguille par une raclette à vitres (un « squeegee ») qui nettoie parfaitement le terrain ![]() :
:
réponse à la question droite cercle géodésique?
Pour clore le débat (intéressant) de ce matin sur le statut des droites et des cercles en géométrie un élément de réflexion comme promis une bd (intelligente) aimablement mise à disposition par l’auteur.
Télécharger (LE_GEOMETRICON.pdf)
et non il y en a plein d’autres que Sophie Germain….quelques exemples
Malgré le prix Poincaré attribué à deux mathématiciennes cet été, les femmes ont du mal à se faire une place dans le monde des mathématiques fondamentales. La parité est lente à se mettre en place et le déséquilibre hommes-femmes s’aggraverait même.
 La parité a du mal à s’installer au sein du monde des mathématiques, encore dominé par les hommes.
La parité a du mal à s’installer au sein du monde des mathématiques, encore dominé par les hommes.
PARITE. L’été dernier, deux jeunes mathématiciennes françaises étaient récompensées par le prestigieux prix Henri Poincaré, mais ces exemples emblématiques masquent, selon plusieurs mathématiciennes interrogées par l’AFP, l’absence persistante de parité dans cette discipline.
Les deux lauréates, Nalini Anantharaman (Laboratoire de mathématiques d’Orsay), 36 ans, et Sylvia Serfaty (Laboratoire Jacques-Louis Lions), 37 ans, sont issues de la même promotion à l’École normale supérieure (1994).
“Il y a une école française remarquable et il y a des femmes remarquables dans cette école française”, convient Aline Bonami, présidente de la Société mathématique de France (SMF). Professeur émérite depuis 2006, cette mathématicienne n’est pas pour autant optimiste quant à l’avenir des femmes en mathématiques, en particulier en “maths pures” ou fondamentales.
“La situation est en train de s’aggraver, alors que dans toutes les autres disciplines la tendance est à avoir davantage de femmes, même si l’évolution est plus ou moins lente”, confirme Laurence Broze, présidente de l’association Femmes et Mathématiques, qui célèbre cette année un quart de siècle d’existence.
Directrice de l’UFR de Mathématiques à l’Université de Lille 3, Laurence Broze dégaine des chiffres: “Il reste aujourd’hui une trentaine de femmes professeurs de mathématiques pures” – contre quelque cinq cents hommes – moitié moins qu’à la meilleure époque.
20-80. En mathématiques appliquées (qui s’intéressent à des problèmes venant d’autres sciences) les femmes tirent un peu mieux leur épingle du jeu, mais cela ne suffit pas à faire bouger les lignes. “Toutes disciplines et grades confondus, on a à l’université 40% de femmes pour 60% d’hommes. En mathématiques, c’est 20% de femmes pour 80% d’hommes”, relève Laurence Broze.
“Extra-terrestre” ou “garçon manqué”
Les femmes n’auraient-elles pas la bosse des maths ? Il faut plutôt chercher ailleurs les raisons de cette inéquation. Et d’abord dans le poids des stéréotypes. Nalini Anantharaman, qui a cumulé l’annonce de son prix et la naissance de son second enfant, pointe “l’image des femmes dans la société”. “Une femme mathématicienne, c’est soit un extra-terrestre, soit un garçon manqué”, analyse-t-elle. Les parents, puis les enseignants, ont un rôle essentiel à jouer pour surmonter cet obstacle, selon elle.“On sait qu’à niveau égal, les filles se sous-estiment”, renchérit Sylvia Serfaty.
DÉCROCHEMENT. Autre explication, le “manque de modèles” féminins, renchérit Laurence Broze. Mais il y a surtout des causes spécifiques à la discipline. Les mathématiciennes interrogées citent en premier lieu la règle de la mobilité instituée par la communauté: chaque promotion – maître de conférence, professeur – nécessite un changement de lieu.
“En mathématiques, la période dont on dit qu’elle est la plus féconde, c’est entre vingt et trente-cinq ans”, explique Laurence Broze. On devient professeur plus tôt que dans d’autres disciplines, à un moment où le compagnon assoit sa propre carrière ou quand arrivent les enfants. “Il y a des petits décrochements de carrière qu’on paie et qui ne se rattrapent pas forcément”, ajoute Sylvia Serfaty.
MODÈLES. Contre toute attente, Aline Bonami estime qu’un modèle masculin comme Cédric Villani peut être un atout. “Le fait qu’il se présente hors des sentiers ordinaires sous certains aspects montre qu’il y a un espace de liberté dans notre métier”.
LE MONDE | | Par Stéphane Foucart

La discrète scientifique de 39 ans, benjamine de l’académie des sciences, est l’une des plus brillantes de sa génération
Un jour, en classe de première, Laure Saint-Raymond a obtenu la note de 14 sur 20 à un devoir de mathématiques. Le visage marqué par la stupeur et l’incrédulité, le professeur – un polytechnicien qui avait choisi l’enseignement – lui rendit sa copie en confessant ne pas comprendre ce qui avait pu se produire. L’événement fut si exceptionnel qu’il demeure imprimé dans la mémoire de ses camarades de classe (parmi lesquels l’auteur de ces lignes) : jamais l’intéressée n’avait connu un écart aussi extravagant avec la note maximale. Personne, d’ailleurs, n’avait jamais pensé que ce fût un jour possible.
Cette minuscule entorse à la perfection n’a pas dû se reproduire souvent dans la carrière de Laure Saint-Raymond. Une vingtaine d’années plus tard, elle est, à 39 ans, reconnue par ses pairs comme une des mathématiciennes les plus brillantes de sa génération. Normalienne et d’abord recrutée par le Centre national de la recherche scientifique, elle est nommée professeure à l’université Pierre-et-Marie-Curie, à 26 ans, âge où le commun des mortels peut espérer soutenir une thèse. Elle est, depuis 2007, directrice adjointe du département mathématiques et applications de l’Ecole normale supérieure de la rue d’Ulm, à Paris. Elle est aussi la benjamine de l’Académie des sciences, élue, fin 2013, à l’âge de 38 ans.
Un choix tardif
Malgré ce qui ressemble bien à une sorte de prédestination (ses parents enseignent les mathématiques), Laure Saint-Raymond n’a choisi que tardivement la voie des maths. « Je me suis finalement décidée le jour où je me suis lancée dans ma thèse, mais j’ai longtemps pensé à faire plutôt carrière dans la musique », dit-elle.
Au lycée, elle venait parfois avec son violoncelle. L’étui était presque aussi grand qu’elle. Ses camarades la harcelaient copieusement pour qu’elle accepte de jouer, au beau milieu de la cour. Par pudeur peut-être, elle refusait obstinément, et n’a cédé qu’une seule fois, pour exécuter les premières mesures d’une suite de Jean-Sébastien Bach qui ont suffi à persuader son auditoire qu’elle était certainement aussi douée avec un violoncelle que devant une équation. « J’ai eu le bonheur de jouer une fois avec elle, raconte le mathématicien Jean-Yves Chemin (université Pierre-et-Marie-Curie), qui fut aussi l’un de ses professeurs. Je puis vous dire qu’elle est une musicienne merveilleuse. »
Maths et sciences de la matière
Le domaine de recherche de Laure Saint-Raymond est un monde où se chevauchent les mathématiques et les sciences de la matière. Où les lois de la nature s’incarnent dans de cabalistiques équations qui deviennent, en elles-mêmes, des objets mathématiques pourvus d’une vie autonome, et dont les propriétés racontent les réalités cachées du monde physique. L’une de ses contributions récentes, conduite notamment avec le mathématicien François Golse (Ecole polytechnique), a été de chercher à retrouver, à partir des lois régissant le mouvement individuel de particules microscopiques, les équations qui décrivent l’écoulement d’un fluide macroscopique.
L’exercice peut sembler parfaitement abscons au béotien, mais il nargue les matheux depuis un certain temps. En 1900, au Congrès international des mathématiciens, l’Allemand David Hilbert (1862-1943) déclarait déjà qu’il fallait chercher « des méthodes fondées sur l’idée de passage à la limite qui, de la conception atomique, nous conduisent aux lois du mouvement des milieux continus »…
Une discipline sans esbroufe
Avec la mathématicienne Isabelle Gallagher (université Paris-Diderot-Paris-VII), Laure Saint-Raymond s’est penchée sur des problèmes en apparence plus terre à terre, mais tout aussi diaboliquement difficiles. « Isabelle et Laure ont travaillé sur des modèles de circulation océanique, sur la difficulté à y intégrer la force de Coriolis , dit Jean-Yves Chemin. Auparavant, nous étions capables de décrire les choses aux latitudes moyennes ; elles sont parvenues à traiter mathématiquement ce qui se produit au voisinage de l’équateur. Le travail qu’elles ont mené sur ce sujet est magnifique. »
Comment une femme jeune perce-t-elle dans un monde plutôt dominé par des hommes âgés ? La chance des mathématiciennes est peut-être qu’elles naviguent dans une discipline où l’esbroufe n’est pas possible. « Je n’ai jamais ressenti la moindre discrimination, dit-elle. Cela ne veut pas dire qu’il n’y a pas de problèmes : en maths, nous sommes loin de la parité. A Normale, nous étions six filles sur les quarante étudiants de ma promotion et c’était, de ce point de vue, une situation plutôt exceptionnelle. Ces dernières années, il y a plutôt une ou deux filles par promotion, guère plus. »
Pourtant, elle ne mâche pas ses critiques devant certaines mesures prises pour favoriser l’accès des femmes aux mathématiques. Un jour, à la cérémonie de remise d’un prix scientifique, un ministre explique qu’il va imposer la parité aux comités de sélection – pensant peut-être que ces comités fonctionnent sur un modèle simple où les hommes choisissent des hommes et les femmes, des femmes. « Je lui ai dit que c’était la mesure la plus contre-productive qu’il était possible de prendre, dit-elle. Puisque les mathématiciennes sont déjà peu nombreuses, elles auront une probabilité plus forte d’être contraintes de participer à ces comités et c’est autant de temps qu’elles n’auront pas pour faire des maths, pour travailler, pour avancer. » Pour être reconnues, en somme. Car, dans les sciences en général et dans les mathématiques en particulier, la reconnaissance ne vient qu’avec les publications.
Le ministre en fut un peu vexé. Discrète et peu attirée par les feux de la rampe, la mathématicienne n’en a pas moins un caractère bien trempé, et une franchise parfois un peu abrupte. « Il est vrai que j’ai un peu de mal à ne pas dire ce que je pense », confesse-t-elle. Mais, après tout, ce petit travers est aussi une qualité.

Pour Julia Kempe, chercheuse au CNRS et élue Femme en Or cette semaine, les femmes s’interdisent trop souvent de se lancer dans les métiers scientifiques, pourtant vecteurs de «liberté et de plaisir».
Elle a un CV de douze pages, parle six langues et ses connaissances sont compilées dans deux thèses. A 36 ans, Julia Kempe, fraîchement promue Femme en Or dans le domaine de la recherche , incarne le visage encore trop méconnu de la science au féminin.
Son «profil atypique» a retenu l’attention du jury qui «s’étonnait que l’on n’ait pas plus parlé d’une scientifique qui a quand même reçu le prix Irène Joliot-Curie en 2006». Le Trophée de la femme en or est donc autant une «consécration» pour ses travaux menés en informatique qu’un «coup de pouce» pour aider l’ascension professionnelle de la scientifique, explique-t-on du côté des organisateurs.
Le gène des maths, Julia Kempe le porte dans son ADN depuis toute petite. Pour cette Berlinoise aux trois nationalités française, allemande et israélienne -, l’héritage familial a été déterminant. Ses parents scientifiques ont largement balisé son terrain de jeux numériques : «Je leur demandais souvent d’imaginer des puzzles mathématiques pour que je puisse les résoudre», se souvient-elle. La méthode marche puisqu’elle rafle tous les concours de logique pendant ses années de collège et lycée, qu’elle passe en ex-RDA.
«Une question de caractère»
Quoi de plus naturel, avec de telles prédispositions, que de s’engager dans des études de maths et de physique ? Sur les bancs de l’Université de Vienne, en Autriche, elle dit avoir côtoyé «un pays traditionnel où les filles sont moins encouragées à étudier les sciences qu’en France.» Au cours de sa carrière, sa condition de femme ne lui a pourtant jamais porté préjudice. Si les profils féminins ne sont pas légion en sciences, c’est aussi «une question de caractère», insiste-t-elle. «Elles n’osent pas, parce que la recherche a la réputation d’être très prenante, donc difficilement conciliable avec la vie de famille. Mais la science, c’est avant tout de la liberté et du plaisir, les femmes sont faites pour ça !», assure-t-elle. Avec le temps, une chercheuse peut même faire son miel de son statut de femme : «Nous sommes rares, alors on se souvient plus facilement de nous, on nous invite plus souvent aux congrès.»
Sa marotte depuis quinze ans : les calculs quantiques. Elle y a consacré deux thèses, réalisées en quatre ans pour le compte de l’Université Berkeley, aux Etats-Unis et l’école ParisTech. A terme, les algorithmes qu’elle développe pourraient permettre de concevoir les ordinateurs du futur, des machines quantiques très puissantes.
Ses contacts à l’Université de Berkeley lui auraient permis d’envisager une carrière outre-Atlantique, mais Julia Kempe ne fait pas partie de ces chercheurs attirés par l’eldorado américain. Depuis 2001, elle officie au laboratoire informatique d’Orsay, sous la houlette du CNRS, et elle y trouve son compte. Vantant «la grande liberté que cette maison donne aux chercheurs», elle apprécie ses horaires très souples, qui lui permettent de travailler la nuit lorsqu’elle «ne trouve pas d’idées le jour» et une obligation d’enseignement réduite a minima avec seulement trois heures de cours hebdomadaires. Une approche qui n’est pas celle des Etats-Unis, «qui fonctionne plus par objectifs» et où le quota d’heures d’enseignement est plus important. «Moi je voulais du temps pour mes recherches et puis la science fondamentale ne doit pas dépendre de plannings.»
Depuis quelques mois, Julia Kempe a cependant moins les mains libres : «J’attends un enfant pour le mois de septembre», confie-t-elle. Alors la future mère aménage son train de vie, reste un peu plus chez elle, correspond par email au lieu de se déplacer… La trentenaire a bien conscience qu’une naissance peut représenter un obstacle pour une carrière de scientifique : «Je l’ai vu chez des collègues qui ont eu un enfant juste après leur thèse.» Un moment critique selon elle, où le chercheur doit produire beaucoup d’efforts pour faire connaître son travail et gagner la reconnaissance de ses pairs. «Heureusement pour moi, je ne commence pas ma carrière», lâche-t-elle.
Une mathématicienne hors norme, combattons les clichés!
Sophie Germain, femme mathématicienne au génie méconnu
Alicia Filks vous présente Sophie Germain, une femme mathématicienne du XVIII ème siècle qui a lutté contre la société de son temps pour imposer ses travaux.

Dans la vie, je fais des maths. Chacun ses tares, me direz-vous : il n’empêche que je kiffe. Seulement voilà… au fur et à mesure que mon compteur Bac+n s’incrémentait, j’ai pu constater que le ratio femmes/hommes de mes promos s’amenuisait dangereusement. Si bien que je me suis assez vite retrouvée à être la seule fille au sein d’une classe de matheux.
Et croyez-moi, on se sent parfois bien seule . J’admets qu’entre mes cours de théorie des nombres et de cryptographie symétrique, ou même d’histoire des mathématiques, la question « Mais elles sont où, bon sang, toutes les nanas qui font des maths ? » ne me venait pas si souvent à l’esprit. Et c’est bien dommage !
Du coup, j’ai souhaité vous parler de ma rencontre accidentelle avec une mathématicienne de renom. Comme ça, quand on vous demandera d’un ton condescendant « Attends, mais hormis Marie Curie tu peux me citer une femme de sciences qui a changé le monde ? », vous pourrez répondre plus facilement sans l’aide de Google.
Ma rencontre avec Sophie Germain
Quand je dis que cette rencontre était accidentelle, je n’exagère rien.
Sophie Germain, je l’avais croisée à plusieurs reprises : une rue de Paris porte son nom, tout comme une certaine catégorie de nombres premiers que je manipule régulièrement. Remarquez, ça aurait pu me mettre la puce à l’oreille, en mode « Youhouuuu y a des NOMBRES qui s’appellent comme une MEUF, t’as pas envie d’en savoir plus ? », mais que voulez-vous, je m’attachais plus à leur manipulation parce qu’ils sont un petit peu relous à trouver. Y a même un cratère de Vénus qui porte son nom ! Malgré tout cela je ne m’étais jamais intéressée de plus près au personnage de Sophie Germain : pour moi, c’était un nom, sans plus.
Et puis un jour j’ai changé de fac et j’ai eu cours dans un bâtiment appelé Sophie Germain. Un bâtiment de maths. J’ai donc posé mon sac deux secondes (après je l’ai ramassé, faut pas déconner, il est crade le parvis de la fac), j’ai bu une gorgée de mon thé d’un air songeur — le même que celui du flic qui arrive sur une scène de crime dans une série américaine des années 2000. Je me suis cramé la langue et j’ai pensé « Hmmmm… C’est qui elle, j’ai déjà entendu son nom quelque part… » (oui, bon, je ne maîtrise pas vraiment l’art de la punchline mentale non plus).
La machine était lancée ! J’ai filé dans la salle de cours, et j’ai googlé, googlé, googlé jusqu’à plus soif (de thé). Et j’ai découvert un drôle de bout de femme.

Eh beh dis donc.
Sophie Germain, c’est un peu Mulan, mais en France
Sophie Germain est née à Paris en 1776 et a montré très tôt un goût certain et un talent fou pour les mathématiques. À l’âge de 13 ans, la jeune fille lit l’histoire de la mort d’Archimède ; on raconte que c’est parce qu’elle était émue par ce récit qu’elle a pris la décision de devenir mathématicienne. Ses parents ne kiffaient pas trop l’idée que leur progéniture femelle s’intéresse aux mathématiques, et dans un premier temps ils se sont employés à la dissuader de poursuivre dans cette voie.
Elle s’est donc chargée elle-même de son éducation mathématique toute son adolescence. Du fin fond de ses couettes, en pleine nuit et à l’insu de ses parents, la jeune fille apprend, lit les travaux d’Euler ou de Newton, refait des preuves dans son coin… Si bien qu’à l’aube de ses 20 ans, ses parents, et surtout son père, finissent par accepter de l’aider à s’instruire.
Le problème, c’est qu’à l’époque, la meilleure école mathématique en France n’est autre que l’École Polytechnique, qui vient tout juste d’être créée. Pourquoi c’est un problème ? C’est une école militaire, donc réservée aux hommes. Qu’à cela ne tienne : Sophie Germain réussit quand même à subtiliser des notes de cours donnés à l’X (autre petit nom de l’Ecole Polytechnique).
À l’époque, il n’y avait bien sûr ni scanner, ni photocopieuse et encore moins d’Internet pour lui faciliter la tâche — tout juste des pigeons voyageurs, et encore… Pour y arriver, elle s’est fait passer pour un ancien élève de l’École, Antoine Auguste Leblanc. Cet élève est d’ailleurs décédé quelques années plus tard, et Sophie Germain a gardé son nom.
Mais ça ne s’arrête pas là. Soucieuse de s’améliorer, et parce que la communication et les échanges sont primordiaux pour les mathématiciens, elle décide, sous son nom d’emprunt, de communiquer ses remarques et ses idées à l’un des piliers des mathématiques du dix-neuvième siècle, Joseph-Louis Lagrange, alors professeur à l’École Normale. Il s’agit de l’autre école où l’on peut faire des maths de haut niveau, qui tout comme Polytechnique vient tout juste d’être créée — merci la Révolution !
Une mathématicienne d’exception
Les deux mathématiciens entament alors une longue correspondance. L’intelligence de ce monsieur Leblanc intrigue tellement Lagrange qu’il le convoque… Et se rend compte du subterfuge de la jeune femme. Plutôt que de s’indigner d’avoir été berné de la sorte, il choisit de la soutenir dans ses travaux, admiratif devant le courage dont cette femme fait preuve.

(Presque) Sophie Germain.
Par la suite, elle est amenée à étudier un problème très célèbre par sa difficulté, le Grand Théorème de Fermat (qui vient tout juste d’être résolu, il y a quelques années, après trois siècles de prises de tête) et entame donc une correspondance, toujours sous le nom de Leblanc, avec Karl Friedrich Gauss.
Si ce nom ne vous dit rien, je vous invite à demander à un•e de vos ami•e•s qui fait un peu de maths de vous expliquer le théorème de Gauss. Il y a de grandes chances pour que, les yeux humides et la lèvre inférieure tremblante, il ou elle vous demande « … Lequel ? ». Vous pouvez aussi consulter cette micro liste ; dites- vous bien qu’ils ne sont pas tous répertoriés.
Gauss apprécie grandement sa correspondance avec ce monsieur Leblanc. Et croyez-moi : ce mec, pour l’impressionner, il fallait envoyer du pâté, quand on sait qu’il était réputé pour envoyer bouler nombres de mathématiciens qui, des étoiles dans les yeux, lui présentaient le résultat de plusieurs années de recherches pour finalement se faire laminer d’un « Hmm ? Ah ouais, j’avais démontré ça il y a dix ans mais c’est pas intéressant en fait comme résultat ».
Quand Napoléon envahit la Prusse, Sophie Germain, soucieuse du sort du professeur, charge un général de sa connaissance de la protection de son ami. Ce général finit par dévoiler la véritable identité de la jeune femme, ce qui amène Gauss à lui écrire cette lettre, commençant ainsi :
« Mais comment vous décrire mon admiration et mon étonnement à voir mon estimé correspondant Monsieur Le Blanc se métamorphoser en cet illustre personnage qui donne un si brillant exemple de ce que j’aurais trouvé difficile à croire. Le goût pour les sciences abstraites en général et surtout pour les mystères des nombres est fort rare : on ne s’en étonne pas ; les charmes enchanteurs de cette sublime science ne se décèlent dans toute leur beauté qu’à ceux qui ont le courage de l’approfondir.
Mais lorsqu’une personne de ce sexe, qui, par nos mœurs et par nos préjugés, doit rencontrer infiniment plus d’obstacles et de difficultés, que les hommes, à se familiariser avec ces recherches épineuses, sait néanmoins franchir ces entraves et pénétrer ce qu’elles ont de plus caché, il faut sans doute, qu’elle ait le plus noble courage, des talents tout à fait extraordinaires, le génie supérieur. »
Mulan peut aller se rhabiller ! (Non en vrai, tu restes mon héroïne Disney préférée.)
Concernant le Grand Théorème de Fermat, alors qu’à l’époque tout espoir semblait perdu concernant sa résolution, la mathématicienne parvient à établir le premier résultat significatif.
Puis Sophie Germain délaisse les mathématiques pures pour s’intéresser à la physique ; elle se prend d’ailleurs régulièrement la tête avec Poisson, un de ses contemporains, qui ne prend pas les résultats de la jeune femme au sérieux. Et pourtant ! Son mémoire sur les vibrations des plaques élastiques (des tambours, si on veut enlever le blabla scientifique) va jeter les bases de la théorie modernes de l’élasticité.
À lire aussi : Tribulations d’une doctorante en physique
Maryam Mirzakhani, première femme à recevoir la médaille Fields
Une profession qui lui sera refusée jusqu’au bout
Et c’est un peu ça, la carrière de Sophie Germain. Elle ne sera jamais vraiment prise au sérieux par la majorité de la communauté scientifique, et sera un mouton noir de la société avec son statut de femme savante, un personnage moqué et dénigré. On lui reproche son manque de rigueur et sa tendance à la dispersion, alors qu’elle est constamment ralentie dans ses travaux et n’est pas considérée comme un interlocuteur légitime par ses homologues masculins.

Elle est tellement marginalisée dans la société qu’elle restera une charge à vie pour sa famille : elle ne s’est jamais mariée et ne peut pas gagner sa croûte avec ses recherches, n’étant pas considérée comme une véritable scientifique.
Elle est cependant la première Académicienne à obtenir son titre autrement que par un statut marital. Ses travaux en Théorie des Nombres et des Surfaces ont changé le paysage scientifique de son époque — ses résultats sont d’ailleurs encore mis à contribution de nos jours. C’est la seule personne pour qui Gauss se battra afin qu’elle obtienne un grade honorifique à l’Université de Göttingen…
Cependant l’Université ne pourra jamais lui accorder ce grade car Sophie Germain meurt d’un cancer du sein en 1831, avant la cérémonie. Et sur son certificat de décès, comme dernière ingratitude, on peut lire : « Sophie Germain, rentière-annuitante », soit femme célibataire sans profession.
réponse à la question le mètre
En réponses aux questions pertinentes sur le mètre (un peu de culture)
si vous voulez aller plus loin lire le livre de Ken Alder “mesurer le monde” qui relate l’aventure de nos deux scientifiques ou le livre de Denis Guedj “Le Mètre du monde” (ces livres sont en poche ou en epub.)
bonne lecture ou recherches ![]()
pour les plus curieux et qui sait pour ouvrir la discussion sur le statut des erreurs dans la sciences en prévision de la terminale je vous joint cet excellentissime article de Mme Laurence Bianchini, Physicienne
Mesure du 1er mètre : une erreur qui changea le monde
Pendant la période agitée de la révolution française deux scientifiques, Méchain et Delambre, furent chargés par le gouvernement révolutionnaire de mesurer la circonférence de la Terre. A partir de cette mesure universelle, les scientifiques ont défini la base du système métrique aujourd’hui utilisé par plus de 95 % de la population mondiale. L’histoire de cette aventure scientifique de sept ans ponctuée d’évènements tragiques montre que la ténacité, la confiance en soi et les erreurs sont des paramètres souvent ignorés mais qui contribuent aussi à l’établissement des connaissances scientifiques.
Il y a quelques années, Ken Alder, professeur d’histoire des sciences à l’université de Northwestern près de Chicago, a retrouvé les notes écrites de ces deux scientifiques français. Ces manuscrits présumés disparus depuis longtemps se trouvaient pour l’un dans les archives de l’Observatoire de Paris, pour l’autre dans une bibliothèque de l’état de l’Utah aux Etats-Unis. Dans son livre « Mesurer le Monde, l’incroyable histoire de l’invention du mètre » publié en 2004, Ken Alder relate ce voyage tant historique que scientifique ponctué de tragédies humaines. Grâce à son regard d’épistémologue, nous redécouvrons la Science sous les traits d’une aventure avant tout humaine. L’histoire et le contexte social de ce récit proposent aussi de questionner certains ‘outils’ communs de notre quotidien comme le mètre, l’erreur et l’incertitude scientifique.
En 1792, Jean-Baptiste Delambre et Pierre Méchain, deux astronomes de renom, partirent de Paris dans deux directions opposées afin de mesurer la taille de la Terre. Le gouvernement révolutionnaire français (Convention Nationale) fraîchement élu leur avait confié la mission de mesurer précisément la partie du méridien terrestre reliant Dunkerque à Barcelone et passant par la capitale française. Dans quel but? Pour réformer le système de mesure « pour tous pour toujours ». Dans cette ambiance révolutionnaire, leur ambition était de transformer la vie du peuple français et de les libérer du joug social de la monarchie. La monnaie, le calendrier, la semaine de sept jours et même l’heure de 60 minutes n’y coupèrent pas. Ils avaient en outre besoin de définir une nouvelle unité unique afin d’harmoniser les systèmes de mesure et d’ouvrir le marché du commerce. « Lors de transactions, les gens dépendaient d’une tierce personne qui calculait les quantités qu’ils vendaient et achetaient. Condorcet aurait dit à propos du mètre que [je cite] : « Le peuple ne sera jamais libre tant que les gens ne pourront calculer.» A l’époque, il existait environ 250 000 unités de poids et de longueur : le pied, le point, le pouce, la ligne, la perche… Certaines différaient même d’une province à l’autre, souvent pour accommoder les intérêts des seigneurs locaux. D’ailleurs, la plupart des « cahiers de doléances » de l’époque demandaient l’établissement d’une unité de mesure unique.

La mission de ces deux astronomes avait donc une importance philosophique et éthique. Dans son livre, Ken Alder décrit le voyage des deux hommes, les difficultés qu’ils durent surmonter, les rencontres effectuées… Alors qu’ils gravissaient avec d’étranges instruments des volcans éteints, des tours d’églises et de cathédrales, les obstacles que les hommes leur opposèrent furent les plus contraignants. Ils ont été parfois emprisonnés et accusés d’être des espions, des royalistes ou des sorciers. Lors de son périple, Méchain fut aussi grièvement blessé. Lorsque Ken Alder parcouru les notes des deux scientifiques, il découvrit un élément des plus surprenants. Méchain séjournait à Barcelone dont il venait de mesurer la latitude lorsque, le 7 Mars 1793, l’Espagne déclara la guerre à la France. Méchain fut alors sommé de rester sur la péninsule ibérique. Il mit à profit cette détention pour recalculer la latitude de la ville catalane. Malheureusement pour lui, sa seconde mesure ne coïncidait pas avec la première. Il ne put par la suite jamais renouveler cette mesure et rentra en France dans un état de stress qui vira à la dépression. Le moral de cet homme intègre en fut affecté au point de ne plus vouloir finir la mission qui lui avait été confiée. Il refusa de rendre publiques ses mesures.

- Jean-Baptiste Delambre, French mathematician and astronomer. source : Wikipédia
« Méchain ne possédait aucun concept pour évaluer les erreurs scientifiques. Il savait que les mesures n’étaient jamais parfaites mais les scientifiques de l’époque ne pouvaient pas faire la distinction entre précision et exactitude. Il pensait avoir fait une erreur qu’il considérait comme une défaillance morale, » explique Alder. Finalement, Méchain dévoila son premier lot de mesure mais garda le silence sur les secondes mesures. Le mètre fut ainsi calculé comme étant une fraction (un dix millionième) de la distance entre le Pôle Nord et l’Equateur.* Ceci fut effectué par le plus important rassemblement de scientifiques de l’époque dont Laplace, Legendre et Lagrange. Ceci fut certainement le premier congrès scientifique international de l’histoire des sciences. Un mètre-étalon en platine fut alors fabriqué pour servir de référence pour un système de mesure universel. Après la Révolution, Napoléon Bonaparte aurait dit à propos du mètre : « Les conquêtes viennent et repartent mais ceci perdurera. »
C’est une petite note manuscrite rédigée par Delambre dans le carnet de Méchain, après la mort de celui-ci, qui permit la découverte de l’erreur commise dans son calcul de la latitude de Barcelone. « Delambre, explique Alder, a écrit dans la marge qu’il avait choisi une des deux versions des données de Méchain mais qu’il n’en informerait pas le public car il n’avait pas besoin de le savoir. »
“Parce qu’après tout, est-ce important si cette mesure est fausse ? Le mètre peut-il être faux ?”
En découvrant cette erreur, nous pouvons questionner l’intérêt du voyage des deux scientifiques. Dans son ouvrage, Ken Alder nous livre une réponse contemporaine à cette interrogation. Car en effet, il semblerait que cette période ait vu l’éclosion de nouveaux concepts scientifiques en lien avec cette histoire. Les scientifiques ont par exemple réalisé que la Terre n’était pas une sphère parfaite et qu’elle était aussi plus petite que prévu.

Après la mort de Méchain, Delambre prit possession de ces carnets. Il fit alors face à un sérieux dilemme. Mais entre-temps, des mathématiciens comme Legendre et Gauss avaient développé de nouvelles méthodes pour traiter les données, notamment la « méthode des moindres carrés » qui permet de comparer des données expérimentales entachées d’erreurs de mesure à un modèle mathématique. Cette méthode permet de minimiser l’impact des imprécisions d’une mesure. L’expédition pour ‘la mesure de la Terre’ a ainsi accentué l’importance de la méthode scientifique à une époque où les statistiques n’existaient pas encore. Le hasard joue en effet souvent un rôle prépondérant dans la découverte scientifique . Cette entreprise généra plusieurs avancées scientifiques majeures. Elle servit aussi d’outil politique efficace. Elle permit de modifier la manière de penser des gens et prépara une nouvelle ère du commerce ouvert et international.
Ken Alder évoque un exemple frappant : « En 1999, la NASA a perdu son orbiteur Mars Climate. Il semblerait que la cause de cet accident soit une discordance entre les unités de longueur utilisées par deux équipes travaillant sur le projet. Le système de contrôle des erreurs a échoué dans la détection de celle-ci et l’orbiteur a foncé à grande vitesse contre la surface de Mars. » Depuis 1983, le mètre est défini comme « la distance parcourue par la lumière dans le vide pendant une durée de temps de 1/299 792 456ième de seconde. » Mais il est resté plus court de 0.2 millimètre que le dix millionième d’un quart de méridien du mètre ‘initial’. Il existe donc une erreur scientifique historique qui fait encore aujourd’hui part de notre système de longueur. Une découverte scientifique n’est jamais aussi simple qu’elle le paraît. Elle est construite à partir d’approximations et d’erreurs. Avec cette notion, nous prenons alors conscience que tout ce qui pour nous est un standard, ne l’est pas forcément, ou ne l’a pas toujours été.
Le livre de Ken Alder a été traduit en de nombreuses langues dont le français (voir l’encadré ci-dessous). Il a reçu de nombreux prix et des critiques très positives de la part de la Société de l’Histoire des Sciences et des revues littéraires.
* Finalement, les scientifiques en charge de la définition du mètre choisirent d’utiliser des mesures d’un méridien plus long effectuées 50 ans auparavant. En effet, si la Terre n’est pas sphérique, les méridiens diffèrent alors tous. Ainsi, plus la mesure sera longue plus elle sera précise et meilleure sera l’approximation faite.
 La vidéo ne fonctionne pas? Essayez le lecteur flash!
La vidéo ne fonctionne pas? Essayez le lecteur flash!