Un cadeau de Nicole Ferroni sur les maths et leur philosophie, merci à elle.
Catégorie : 23-26
Stage recherche 2016 élèves de seconde
La modélisation mathématique dans tous ses états
épidémies, virus, plantes, astronomie….
du 20 au 24 juin 2016
à l’Université de Pau et des Pays de l’Adour
Le stage MathC2+ qui se déroulera à Pau du 20 au 24 juin 2016 est ouvert aux élèves de 2nde de l’académie de Bordeaux, motivés par les sciences et se destinant à une première S. Il comprendra des conférences, des films, des ateliers sur des thèmes de recherches actuelles et la visite de plusieurs laboratoires de l’université de Pau et des Pays de l’Adour.
La participation au stage est gratuite, les organisateurs du stage prendront en charge :
- L’hébergement à l’internat du Lycée Jacques Monod de Lescar ;
- Les repas, au restaurant universitaire de Pau à midi, à l’internat de Lescar pour le petit déjeuner et le diner ;
- Les déplacements du lieu de résidence à Pau (sur la base d’un trajet SNCF aller-retour), ainsi que durant la semaine de stage.
Inscription au stage
Le nombre de participants à ce stage est limité à 30 élèves de 2nde.
Une petite sélection est donc nécessaire. Une sélection effectuée avec le critère principal la motivation des candidats, mais tiendra compte également de la répartition géographique, de la parité fille-garçons et de critères sociaux. Les enseignants pourront éventuellement être consultés dans certains cas, et une liste d’attente sera constituée.
Pour postuler au stage, il vous suffit de remplir le Formulaire de candidature avant le vendredi 3 juin à 20h. Les questions suivantes visent à estimer votre motivation, nous vous recommandons de préparer vos réponses en avance et de les copier-coller ensuite dans le formulaire :
-
Pourquoi souhaitez-vous faire ce stage ? Qu’est-ce qui vous motive dans ce thème et dans le programme annoncé ?
-
Citez une découverte scientifique ou un domaine de recherche qui vous attire ou vous passionne et expliquez pourquoi.
-
Y a-t-il une actualité ou un personnage scientifique qui vous a marqué-e et dont vous voudriez dire quelques mots ?
Pour tout renseignement complémentaire, veuillez contacter : jacky.cresson@univ-pau.fr
Présentation du stage
Galilée disait que le « grand livre de la nature est écrit dans la langue mathématique ». Cette phrase, bien que discutable, dit à elle seule le pouvoir des mathématiques à modéliser le réel et à déduire de ces modélisations, non seulement le devenir d’un système mais aussi à nous renseigner profondément sur sa nature. Les ondes gravitationnelles en sont un bel exemple.
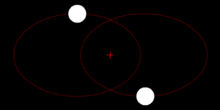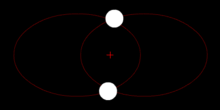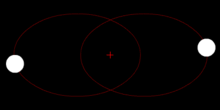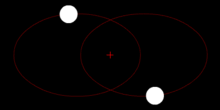
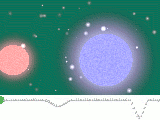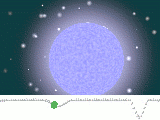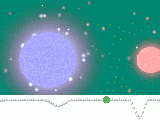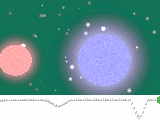
L’objet du stage est de découvrir l’ensemble des outils mathématiques et des questions que soulève la modélisation d’un phénomène réel, que celui-ci appartienne à la biologie comme la propagation d’un virus dans une population, à la physique comme les conséquences d’un séisme ou à l’astronomie avec l’évolution du système solaire.
En particulier, nous aurons quatre étapes bien distinctes à explorer. Chacune de ces étapes fera l’objet d’un des projets de recherche proposés lors de ce stage.
La première étape concerne la construction d’un modèle et sa viabilité, c’est-à-dire le fait que ce modèle respecte un certain nombre de contraintes qui proviennent du domaine étudié et non du cadre mathématique utilisé. Par exemple, lorsqu’on étudie une population, le nombre d’individus doit être entier et positif. Si un modèle produit, à partir d’une population positive, une population négative alors ce modèle n’est pas viable. La construction du modèle demandera de faire des choix que nous discuterons : est-ce un phénomène aléatoire, continu, discret, …? Dans chacun de ces cas, nous poserons la question du respect des contraintes.
Une fois le modèle obtenu, nous chercherons à savoir ce qu’il peut nous dire. La première idée est de rechercher des solutions 
explicites du modèle. Nous verrons que cette recherche est souvent infructueuse et que, même lorsque la solution est connue explicitement, cela ne donne pas forcément accès au comportement futur du système. Nous parlerons à cette occasion de chaos déterministe, des travaux d’Henri Poincaré et de la jungle des fonctions spéciales.
Lorsqu’un résultat théorique est établi, ou lorsque justement aucun résultat ne peut être obtenu dans cette voie, une idée est de produire un modèle numérique du modèle théorique, c’est-à-dire une représentation du modèle théorique qui puisse se mettre sur un ordinateur et permette une étude des différents comportements possibles. Nous étudierons cette procédure et les problèmes qui y sont liés.
 |
 |
Une dernière étape enfin, et non la moindre, est la comparaison à la réalité. Comme les précédentes, nous verrons que celle-ci n’est pas toujours évidente et pose de nouvelles questions de nature mathématique et philosophique.
Nous sommes loin d’avoir aujourd’hui compris tous les problèmes liés à la modélisation et à l’ensemble de ces étapes. Les mathématiciens du futur devront répondre à certaines questions que nous allons mettre en avant durant ce stage. Pourquoi pas vous ?
Les sujets de recherche
du stage MathC2+ 2016
Ces sujets sont à la fois de nature théorique et pratique. En particulier, nous utiliserons les moyens informatiques pour la simulation des modèles et la restitution des résultats.
- Le modèle SIR et la propagation d’un virus : modèle discret pour une épidémie (modèle SIR). Implémentation sur ordinateur. Application sur des données. Développement pour modéliser l’épidémie de la Dengue ou du virus Zika. Application sur les données de la dengue au CAP-VERT en 2009.
- Le modèle logistique en dynamique des populations et le Chaos
- La construction des calendriers et des horloges et les fractions continues : On posera le problème de la construction d’horloge et de calendrier. Ce faisant nous arriverons vers des problèmes d’approximation des nombres réels par les rationnels.
- Forme des virus et polyèdres : les virus possèdent des formes très particulières. En étudiant certains d’entre eux, nous verrons comment l’étude des polyèdres nous permet de déterminer leurs propriétés géométriques et comment ces propriétés influences leurs capacités.
- Les pollens, les formes biologiques et le problème de Tammes : Les cellules biologiques prennent des formes très particulières lorsqu’elles sont soumises à des contraintes. Nous verrons comment rendre compte des différentes formes observées en étudiant le problème de l’empilement de sphères et le problème de Tammes consistant à recouvrir une sphère par de petits disques.
- Les systèmes de Lindenmayer et la modélisation des plantes
- Les fractales et la modélisation de la nature
- La dérive génétique et les probabilités
- Les mathématiques de Google ou comment classer des pages webs : Comment modéliser la recherche d’une page web sur le net ? Comment classer ces pages pour ensuite constituer un moteur de recherche efficace ?
- Le meilleur chemin et le réseau des lignes de bus : Comment modéliser le déplacement entre deux points d’un réseau de villes ou sur le réseau de bus ou de métro ? Comment en déduire un „meilleur“ chemin ?
- La synchronisation des lucioles et les rythmes du vivant
- Le jeu du chaos et l’ADN
Programme de la semaine
du stage MathC2+ 2016
|
Matin |
après-midi |
||
|
Lundi |
Conférence générale et historique sur la modélisation, par J. Cresson, Univ. de Pau et Observatoire de Paris Visite du Laboratoire IPRA et Imprimante 3D |
Présentation des sujets de recherche |
Projection du documentaire Einstein et la Relativité Générale, une histoire singulière de Quentin Lazzarotto |
|
Mardi |
Présentation des formations scientifiques de l’UPPA par Walter Tinsson Conférence De l’infiniment |
Ateliers de recherche |
Atelier origamis et d’autres activités avec le Mathematicum de l’université de Pau |
| Mercredi | Visite du Chateau de Pau | Ateliers de recherches | Projection du film « Pourquoi j’ai détesté les maths » de Olivier Peyon avec Cedric Villani (Médaille Fields 2010). |
|
Jeudi |
Visite du Centre d’Imagerie à rayons X -UPPA CNRS TOTAL |
Ateliers de recherche |
Activité sportive |
|
Vendredi |
Préparation des restitutions orales |
Présentations orales et goûter |
devoir corrigé second degré
exercices corrigés second degré secondes
quelques exercices corrigés
correction dm paraboles et inéquations
Un corrigé à partir de vos travaux
des problèmes d’ordre
Une vidéo intéressante à écouter et à réfléchir est éclairante sur les phénomènes d’ordre même pour la vie courante l’auteur peut être suivi sur youtube.
La vidéo ne fonctionne pas? Essayez le lecteur flash!
encore du second degré
le 
vous souhaite une merveilleuse année
Un mathématicien, un physicien, un informaticien et un littéraire sont devant un problème : montrer que tous les nombres impairs sont premiers.
Le mathématicien dit : « 3 est premier, 5 est premier, 7 est premier, 9 n’est pas premier, donc ça ne marche pas ».
Le physicien dit : « 3 est premier, 5 est premier, 7 est premier, donc en première approximation, ça marche ».
L’informaticien dit : « 3 est premier, 5 est premier, 7 est premier, 9 n’est pas premier, 9 n’est pas premier, 9 n’est pas premier, 9 n’est pas premier,… ».
Le littéraire dit : « C’est quoi, un nombre premier ? ».
réponse à la question le mètre
En réponses aux questions pertinentes sur le mètre (un peu de culture)
si vous voulez aller plus loin lire le livre de Ken Alder “mesurer le monde” qui relate l’aventure de nos deux scientifiques ou le livre de Denis Guedj “Le Mètre du monde” (ces livres sont en poche ou en epub.)
bonne lecture ou recherches 
pour les plus curieux et qui sait pour ouvrir la discussion sur le statut des erreurs dans la sciences en prévision de la terminale je vous joint cet excellentissime article de Mme Laurence Bianchini, Physicienne
Mesure du 1er mètre : une erreur qui changea le monde
Pendant la période agitée de la révolution française deux scientifiques, Méchain et Delambre, furent chargés par le gouvernement révolutionnaire de mesurer la circonférence de la Terre. A partir de cette mesure universelle, les scientifiques ont défini la base du système métrique aujourd’hui utilisé par plus de 95 % de la population mondiale. L’histoire de cette aventure scientifique de sept ans ponctuée d’évènements tragiques montre que la ténacité, la confiance en soi et les erreurs sont des paramètres souvent ignorés mais qui contribuent aussi à l’établissement des connaissances scientifiques.
Il y a quelques années, Ken Alder, professeur d’histoire des sciences à l’université de Northwestern près de Chicago, a retrouvé les notes écrites de ces deux scientifiques français. Ces manuscrits présumés disparus depuis longtemps se trouvaient pour l’un dans les archives de l’Observatoire de Paris, pour l’autre dans une bibliothèque de l’état de l’Utah aux Etats-Unis. Dans son livre « Mesurer le Monde, l’incroyable histoire de l’invention du mètre » publié en 2004, Ken Alder relate ce voyage tant historique que scientifique ponctué de tragédies humaines. Grâce à son regard d’épistémologue, nous redécouvrons la Science sous les traits d’une aventure avant tout humaine. L’histoire et le contexte social de ce récit proposent aussi de questionner certains ‘outils’ communs de notre quotidien comme le mètre, l’erreur et l’incertitude scientifique.
En 1792, Jean-Baptiste Delambre et Pierre Méchain, deux astronomes de renom, partirent de Paris dans deux directions opposées afin de mesurer la taille de la Terre. Le gouvernement révolutionnaire français (Convention Nationale) fraîchement élu leur avait confié la mission de mesurer précisément la partie du méridien terrestre reliant Dunkerque à Barcelone et passant par la capitale française. Dans quel but? Pour réformer le système de mesure « pour tous pour toujours ». Dans cette ambiance révolutionnaire, leur ambition était de transformer la vie du peuple français et de les libérer du joug social de la monarchie. La monnaie, le calendrier, la semaine de sept jours et même l’heure de 60 minutes n’y coupèrent pas. Ils avaient en outre besoin de définir une nouvelle unité unique afin d’harmoniser les systèmes de mesure et d’ouvrir le marché du commerce. « Lors de transactions, les gens dépendaient d’une tierce personne qui calculait les quantités qu’ils vendaient et achetaient. Condorcet aurait dit à propos du mètre que [je cite] : « Le peuple ne sera jamais libre tant que les gens ne pourront calculer.» A l’époque, il existait environ 250 000 unités de poids et de longueur : le pied, le point, le pouce, la ligne, la perche… Certaines différaient même d’une province à l’autre, souvent pour accommoder les intérêts des seigneurs locaux. D’ailleurs, la plupart des « cahiers de doléances » de l’époque demandaient l’établissement d’une unité de mesure unique.
The Borda circle was the instrument used by Delambre and Méchain to estimate the latitudes. source : Abbé J. Loridan, Voyages des Astronomes français à la recherche de la figure de la terre et de ses dimensions
La mission de ces deux astronomes avait donc une importance philosophique et éthique. Dans son livre, Ken Alder décrit le voyage des deux hommes, les difficultés qu’ils durent surmonter, les rencontres effectuées… Alors qu’ils gravissaient avec d’étranges instruments des volcans éteints, des tours d’églises et de cathédrales, les obstacles que les hommes leur opposèrent furent les plus contraignants. Ils ont été parfois emprisonnés et accusés d’être des espions, des royalistes ou des sorciers. Lors de son périple, Méchain fut aussi grièvement blessé. Lorsque Ken Alder parcouru les notes des deux scientifiques, il découvrit un élément des plus surprenants. Méchain séjournait à Barcelone dont il venait de mesurer la latitude lorsque, le 7 Mars 1793, l’Espagne déclara la guerre à la France. Méchain fut alors sommé de rester sur la péninsule ibérique. Il mit à profit cette détention pour recalculer la latitude de la ville catalane. Malheureusement pour lui, sa seconde mesure ne coïncidait pas avec la première. Il ne put par la suite jamais renouveler cette mesure et rentra en France dans un état de stress qui vira à la dépression. Le moral de cet homme intègre en fut affecté au point de ne plus vouloir finir la mission qui lui avait été confiée. Il refusa de rendre publiques ses mesures.
- Jean-Baptiste Delambre, French mathematician and astronomer. source : Wikipédia
« Méchain ne possédait aucun concept pour évaluer les erreurs scientifiques. Il savait que les mesures n’étaient jamais parfaites mais les scientifiques de l’époque ne pouvaient pas faire la distinction entre précision et exactitude. Il pensait avoir fait une erreur qu’il considérait comme une défaillance morale, » explique Alder. Finalement, Méchain dévoila son premier lot de mesure mais garda le silence sur les secondes mesures. Le mètre fut ainsi calculé comme étant une fraction (un dix millionième) de la distance entre le Pôle Nord et l’Equateur.* Ceci fut effectué par le plus important rassemblement de scientifiques de l’époque dont Laplace, Legendre et Lagrange. Ceci fut certainement le premier congrès scientifique international de l’histoire des sciences. Un mètre-étalon en platine fut alors fabriqué pour servir de référence pour un système de mesure universel. Après la Révolution, Napoléon Bonaparte aurait dit à propos du mètre : « Les conquêtes viennent et repartent mais ceci perdurera. »
C’est une petite note manuscrite rédigée par Delambre dans le carnet de Méchain, après la mort de celui-ci, qui permit la découverte de l’erreur commise dans son calcul de la latitude de Barcelone. « Delambre, explique Alder, a écrit dans la marge qu’il avait choisi une des deux versions des données de Méchain mais qu’il n’en informerait pas le public car il n’avait pas besoin de le savoir. »
“Parce qu’après tout, est-ce important si cette mesure est fausse ? Le mètre peut-il être faux ?”
En découvrant cette erreur, nous pouvons questionner l’intérêt du voyage des deux scientifiques. Dans son ouvrage, Ken Alder nous livre une réponse contemporaine à cette interrogation. Car en effet, il semblerait que cette période ait vu l’éclosion de nouveaux concepts scientifiques en lien avec cette histoire. Les scientifiques ont par exemple réalisé que la Terre n’était pas une sphère parfaite et qu’elle était aussi plus petite que prévu.
Pierre Méchain, French astronomer. source : Stoyan R. et al. Atlas of the Messier Objects: Highlights of the Deep Sky
Après la mort de Méchain, Delambre prit possession de ces carnets. Il fit alors face à un sérieux dilemme. Mais entre-temps, des mathématiciens comme Legendre et Gauss avaient développé de nouvelles méthodes pour traiter les données, notamment la « méthode des moindres carrés » qui permet de comparer des données expérimentales entachées d’erreurs de mesure à un modèle mathématique. Cette méthode permet de minimiser l’impact des imprécisions d’une mesure. L’expédition pour ‘la mesure de la Terre’ a ainsi accentué l’importance de la méthode scientifique à une époque où les statistiques n’existaient pas encore. Le hasard joue en effet souvent un rôle prépondérant dans la découverte scientifique . Cette entreprise généra plusieurs avancées scientifiques majeures. Elle servit aussi d’outil politique efficace. Elle permit de modifier la manière de penser des gens et prépara une nouvelle ère du commerce ouvert et international.
Ken Alder évoque un exemple frappant : « En 1999, la NASA a perdu son orbiteur Mars Climate. Il semblerait que la cause de cet accident soit une discordance entre les unités de longueur utilisées par deux équipes travaillant sur le projet. Le système de contrôle des erreurs a échoué dans la détection de celle-ci et l’orbiteur a foncé à grande vitesse contre la surface de Mars. » Depuis 1983, le mètre est défini comme « la distance parcourue par la lumière dans le vide pendant une durée de temps de 1/299 792 456ième de seconde. » Mais il est resté plus court de 0.2 millimètre que le dix millionième d’un quart de méridien du mètre ‘initial’. Il existe donc une erreur scientifique historique qui fait encore aujourd’hui part de notre système de longueur. Une découverte scientifique n’est jamais aussi simple qu’elle le paraît. Elle est construite à partir d’approximations et d’erreurs. Avec cette notion, nous prenons alors conscience que tout ce qui pour nous est un standard, ne l’est pas forcément, ou ne l’a pas toujours été.
Le livre de Ken Alder a été traduit en de nombreuses langues dont le français (voir l’encadré ci-dessous). Il a reçu de nombreux prix et des critiques très positives de la part de la Société de l’Histoire des Sciences et des revues littéraires.
* Finalement, les scientifiques en charge de la définition du mètre choisirent d’utiliser des mesures d’un méridien plus long effectuées 50 ans auparavant. En effet, si la Terre n’est pas sphérique, les méridiens diffèrent alors tous. Ainsi, plus la mesure sera longue plus elle sera précise et meilleure sera l’approximation faite.
